This exercise is an example of how, in programming, there’s often more work in solving a problem mathematically or algorithmically than there is in actually writing code. Before you write any code, start by asking yourself: how would I solve this problem mathematically? Work through a few examples on paper and note the way in which you solve the problem. This is your (admittedly rather simple) algorithm, which you then need to turn into a Python expression.
Background
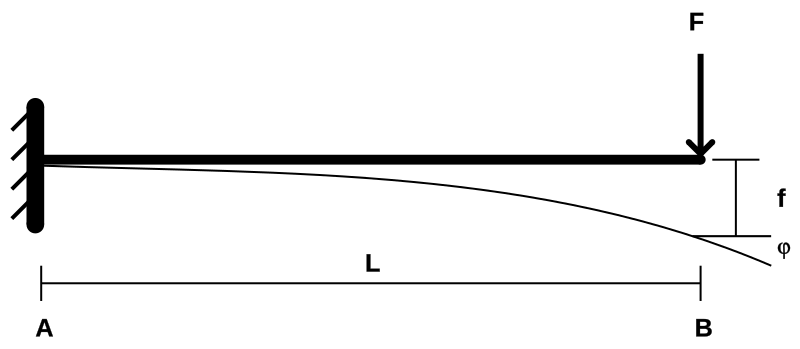
An important consideration in structural engineering is the degree to which structural beams bend or deflect. Although we mostly work with ideal (i.e., non-deforming) structural elements in Engineering One courses such as Statics, real objects bend and break. For example, Figure 1 shows a beam that is cantilevered (one end of it is fixed), with a force applied to the end of the beam.
Figure 1. Force applied to the end of a cantilever
In such a beam, the angle of deflection of the beam $\phi_B$ (in radians) can be calculated as:
\[ \phi_B = \frac{F L^2}{2 E I} \]
where $F$ is the force acting on the beam, $L$ is the beam’s length, $E$ is the beam’s moment of elasticity (a topic beyond us for the moment) and $I$ is its moment of inertia (which you may see in ENGI 1010). This assumes, however, that the beam is weightless — still not a very realistic model! A more exacting model is that of a force applied uniformly along the length of a beam, as shown in Figure 2.
Figure 2. Force applied along a cantilever
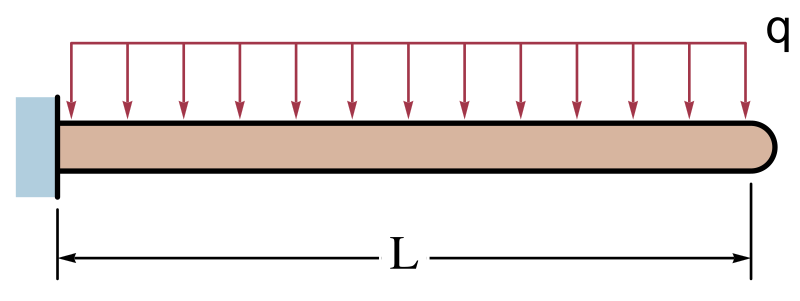
In this model, the angle of deflection at the end of the beam is given as:
\[ \phi_B = \frac{q L^3}{6 EI} \]
where $q$ is the load on the beam ($F \div L$) and the other quantities are as above. The angle of deflection of the beam at a position $x$ along the beam is given by the following equation:
\[ \phi_x = \frac{q x}{6 E I} \left( 3 L^2 - 3 L x + x^2 \right) \]
Objective
Your goal for this exercise is to write a Python expression for the load $q$ on a cantilever under uniform loading. You may assume that the following variables have been defined for you:
| Variable | Meaning | Unit | Constraint(s) |
|---|---|---|---|
|
Length of the beam |
m |
$L > 0$ |
|
Point on the beam where deflection is measured (distance from anchored end) |
m |
$0 \leq x \leq L$ |
|
Angle of deflection at $x$ |
radians (dimensionless) |
$\phi_x \geq 0$ |
|
Pa (N/m2) |
$E > 0$ |
|
|
Area moment of inertia |
m4 |
$I > 0$ |
Procedure
Assuming that the variables described above have been provided for you,
write a Python expression for the load on the beam ($q$).
As in exercise 0,
don’t provide a script or a function, don’t print anything or expect user
input, just write the expression in a file called exercise1.py.
Submit this file to
Gradescope
for functional evaluation.